Fibonacci Sayıları
Fibonacci sayıları, matematiksel bir dizi oluşturan sayılar kümesidir. Bu sayılar, 13. yüzyılda yaşamış olan İtalyan matematikçi Leonardo Fibonacci tarafından keşfedilmiştir. Fibonacci sayıları, matematiksel dünyada büyük bir ilgi görmüş ve birçok alanda kullanılmıştır.
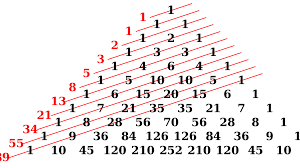
Fibonacci dizisi, her sayının kendinden önceki iki sayının toplamı olduğu bir diziyle başlar. Yani, herhangi bir Fibonacci sayısı, kendinden önceki iki Fibonacci sayısının toplamıdır. Dizinin ilk iki sayısı genellikle 0 ve 1 olarak kabul edilir. Buna göre, Fibonacci dizisi şu şekilde başlar: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
Fibonacci sayıları, birçok doğal olgu ve matematiksel problemlerle ilişkilendirilebilir. İşte Fibonacci sayılarının bazı özellikleri:
1. Altın Oran:
Fibonacci sayıları arasında ilginç bir ilişki olan altın oran, matematik ve sanatta sıklıkla kullanılır. Altın oran, ardışık Fibonacci sayılarının birbirine oranlanmasıyla elde edilir. Bu oran, yaklaşık olarak 1.61803398875 olarak hesaplanır. Altın oran, estetik ve denge arayışında mimaride, resimde ve müzikte kullanılır.
2. Bitişik Sayılar:
Fibonacci dizisindeki ardışık sayılar birbirine yaklaşık olarak oranı 1.618 olan altın orana yaklaşır. Örneğin, 5/3, 8/5, 13/8 gibi. Bu oran, birçok doğal olguda, örneğin bitki yapısında, deniz kabuklarında ve hayvan vücutlarında gözlemlenebilir.
3. Spiral Şekiller:
Fibonacci sayıları, spiral şekillerin oluşumunda da önemli bir rol oynar. Fibonacci sayılarından elde edilen karelerin birleşimiyle oluşan Fibonacci spiraline, doğanın birçok noktasında rastlanır. Örneğin, güneş çiçeklerinin yaprak dizilimi, deniz kabuklarının spiral yapısı ve kasık bölgelerindeki yaprak düzenlemesi gibi.
4. Matematiksel Problemler:
Fibonacci sayıları, birçok matematiksel problemin çözümünde kullanılır. Örneğin, kombinatorik problemler, olasılık teorisi, matematiksel analiz ve sayı teorisi gibi alanlarda Fibonacci sayılarına sık sık başvurulur.
Fibonacci sayıları, matematik dünyasında büyük bir ilgi gören ve birçok alanda kullanılan bir sayı dizisidir. Altın oran, spiral şekiller, doğal olgular ve matematiksel problemler gibi birçok alanda Fibonacci sayılarının önemi ve etkisi gözlenir. Bu sayılar, matematiksel düşünceyi ve problemleri anlamak için temel bir araç olarak kullanılır ve matematiğin derinliklerine dair bir pencere açar.